验证复杂系统中的低秩假设
发布时间：2024-01-25 10:20:17来源：
在一项新的研究中，科学家们研究了复杂系统中普遍存在的低秩假设，证明尽管存在高维非线性动力学，但许多真实网络表现出快速下降的奇异值，支持有效降维以理解和建模复杂系统行为的可行性。
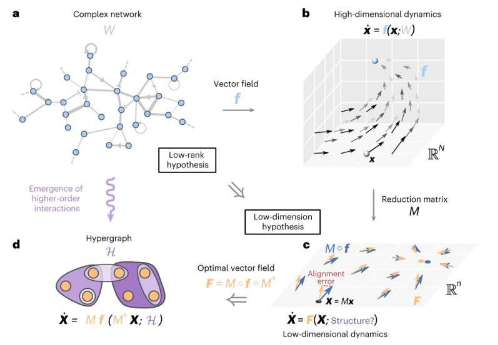
该研究结果发表在《自然物理学》杂志上。
复杂系统是指错综复杂、相互关联的结构或过程，其特征是具有非线性相互作用的众多组件，这使得根据各个部件的属性来预测其行为具有挑战性。
例子包括生态系统、神经网络和社会结构，其中集体相互作用导致涌现现象和自组织。理解复杂系统涉及研究不同尺度的模式、反馈循环和动态行为，对物理学、生物学、社会学和网络科学做出贡献。
由于涉及高维非线性动力学，复杂系统常常给理解其大规模行为带来挑战。现在，由博士 Vincent Thibeault 领导的科学家们。加拿大魁北克拉瓦尔大学的学生旨在通过探索复杂系统的内在简单性并找到简化模型的最佳维度来应对这一挑战。
“通过阅读有关该主题的大量论文，从网络科学到神经科学，帕特里克和我发现，很明显，在用于描述真实网络和交互的矩阵上存在一个低阶假设。许多高维非线性动力系统。”
免责声明：本答案或内容为用户上传，不代表本网观点。其原创性以及文中陈述文字和内容未经本站证实，对本文以及其中全部或者部分内容、文字的真实性、完整性、及时性本站不作任何保证或承诺，请读者仅作参考，并请自行核实相关内容。 如遇侵权请及时联系本站删除。
